
Python : Intersection de deux segments.
Introduction
Ce document décrit un algorithme pour calculer le point d'intersection entre deux segments. Cette méthode s'appuie sur le principe présenté par Paul Bourke à l'adresse suivante : http://local.wasp.uwa.edu.au/~pbourke/geometry/lineline2d/
La méthode de calcul
Dans un premier temps, on pose l'équation du point d'intersection sur le segment AB, PAB, ainsi que du point d'intersection PCD
situé sur le segment CD :
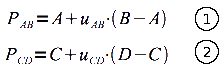
Le point d'intersection se trouve sur le segment, entre le point A et B. Autrement dit, sa position est égale au point A plus un morceau du segment, c'est-à-dire une fraction de la distance entre A et B. Cette portion de segment correspond à la différence entre le point B et le point A multiplié par un facteur uAB compris entre 0 et 1. Par exemple, si le point d'intersection est placé exactement au milieu du segment AB uAB vaut 0.5.
Les deux points sont identiques, on peut donc poser l'égalité suivante :
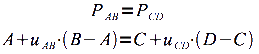
A partir de l'équation n°1 on obtient deux équations à deux inconnues pour les positions x et y :
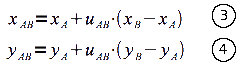
On tire de ces équations les inconnues uAB et uCD :
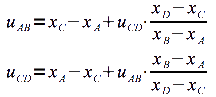
On utilise ces résultats en remplaçant uAB dans l'équation n°1 pour obtenir
la valeur de uCD en fonction des coordonnées des segments. On trouve la valeur de
uAB de la même façon.
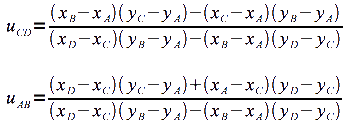
Si les deux segments se croisent, uAB et uCD sont nécessairement compris entre 0 et 1. Pour déterminer la position exacte où les deux droites se croisent on utilise la formule (1).
Dans le cas particulier où le dénominateur est égal à zéro, les deux droites sont parrallèles. Si le numérateur et le dénominateur valent tout deux zéro, les deux segments coïncident.